• Practice constructing and using heap data structure as a priority queue ADT.
• Practice writing merge operation in skew and leftist heap data structures.
• Gain additional experience constructing and using binary trees.
• Practice using recursion in programs.
• Learn to use function pointers.
• Practice writing unit tests.
• Practice working in a Linux environment.
• Practice analyzing and understanding a project requirements.

California’s agricultural regions are the top producers of more than 74 commodities in the US. But they consume about 80% of the water in California. The water shortage in California asks for maximum efficiency in water usage. According to California Department of Water Resources even small improvements in agricultural water usage can be significant. The Department of Water Resources constantly work with all stakeholders to find better solutions for improving the water usage efficiency.

A startup company saw the opportunity and designed a smart irrigation control system for prioritizing the water distribution to the different types of crops based on some factors. The engineers decided to implement the prototype of the system using the following factors:

• Temperature
• Soil moisture
• Plant type
• Time of day

The system collects and updates the information through sensors multiple times a day. You are assigned the task of implementing the priority queue in this system. The system automatically prioritizes the crops for irrigation. The algorithm that uses the criteria to calculate the priorities can change. Therefore, the system should have the possibility of changing the distribution priorities. An algorithm that can determine the priority will be implemented in a function. Such an architecture allows us to use different priority functions.

In this application multiple crops based on proximity are stored in a priority queue. This queue represents a region. Then multiple regions are stored in another priority queue which controls the system. This system prioritizes the irrigation based on the regions priority and crops priority within a region. Therefore, there are two levels of priorities.

Please note, this is a fictional scenario.

Skew Heap

A skew heap is a specialized version of a heap data structure which performs the insertion and deletion operations in O(log n) amortized time. This data structure is a binary tree in which the root always holds the node with the highest priority. Skew heap uses merge operation to perform insertion and deletion.

The major operations supported by a skew heap are insertion of elements, reading the highest priority element, and removing the highest priority element. Reading the highest priority element is just a matter of reading the root node of the heap. The other two operations, insertion and removal, are applications of the merge function:

• To insert a new node x into an existing skew heap H, we treat x as a single-node skew heap and merge it with H.
• To remove the node with highest priority value, we delete the root node and then merge the root's left and right sub-heaps.

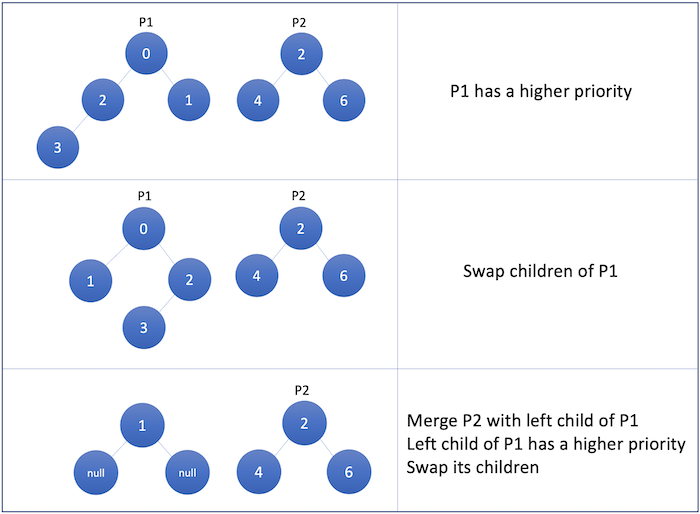
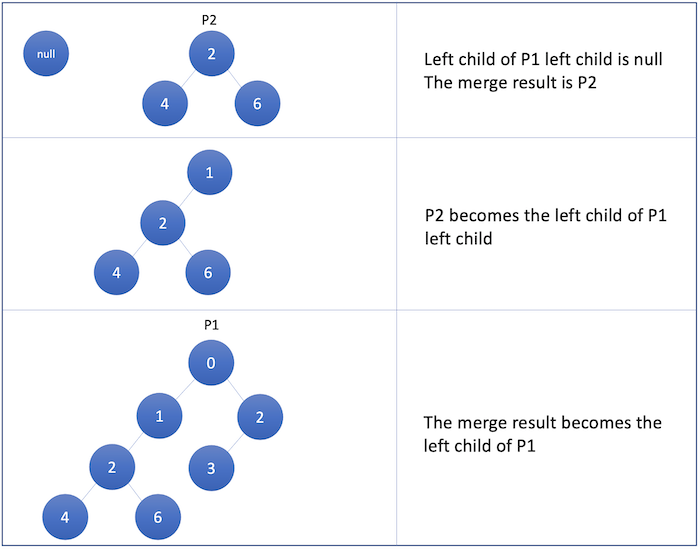
The special feature of a skew heap is the merge operation which combines two skew heaps into a single, valid skew heap. Let p1 and p2 be positions in two skew heaps (e.g. pointers to nodes). The merge operation is defined recursively:

• If p1 is Null, return p2; similarly, if p2 is Null, return p1.
• Assume that p1 has higher priority than p2; if not, swap, p1 and p2.
• Swap the left and right subtrees of p1.
• Recursively merge p2 and the left subtree of p1, replacing the left subtree of p1 with the result of the recursive merge.

Leftist Heap

A leftist heap is similar to skew heap and it uses a merge operation for insertion and deletion. However, it maintains a specific property and it uses the property during the merge operations. Every node in a leftist heap stores a value called Null Path Length (NPL). This value presents the lowest number of edges from the node to a null node. In the other word the NPL value represents the shortest possible path from a node to a null node.

During a merge operation if the NPL value of the right child is larger than the NPL value of the left child we swap the children. This generally makes the left subtree heavier than the right subtree.

In this project, you will implement a priority queue class based on a skew-heap or a Leftist-heap data structure; it can maintain a min-heap or a max-heap based on the computed priority for every node, where the priority function is provided to the queue constructor via a function pointer. Inserting to and extracting from the skew/leftist heap uses a heap merge function which guarantees that the heap property (min-heap or max-heap) is maintained; the comparisons that are part of the merge process will be made on the computed priorities for the objects in the heap. The queue class allows for the priority function to be changed; in which case the heap must be rebuilt. Moreover, the data structure can switch between a skew heap or a leftist heap at the request of the class user. Such a request will trigger reconstruction of the heap.

For this project, you are provided with the following files:

• irrigator.h – The interface for the Crop, and Region classes.
• irrigator.cpp – A skeleton for the implementation of the queue class.
• driver.cpp – A sample driver program. It contains sample use of the queue class.
• driver.txt – A sample output produced by driver.cpp

There are three classes in this project. The class Region has a member variable of type Crop. The class Irrigator has a member of class Region.

Class Crop

The implementation of this class is provided to you. You are not allowed to modify the class. This class stores the following information about a crop:

• m_cropID stores a unique ID for every crop.
• m_temperature stores the temperature at the execution time. The temperature unit is Fahrenheit and it varies between 30 and 110.
• m_moisture stores the moisture of the soil as a percentage for every crop. The moisture values varies between 1 and 100. A value of one indicates complete dryness.
• m_time stores the time of day at the execution. This variable stores time as an index number. The values are morning, noon, afternoon, and night. The morning time is indicated as a zero value.
• m_type stores an index number for every plant type. The plant type is defined as enum in the code. Please refer to irrigator.h to see the list of plants.

Priority Functions

A priority function is a user defined function that can use the information in the class Crop to determine a priority value for a crop. Two example functions are provided in the driver.cpp file. In fact, different plants may have different criteria for this purpose. The ability of using different functions allows us to adapt to different priority algorithms. The heap can accept a prioritization function. This is accomplished by passing a function pointer to the constructor. The function pointer is the address of a function that will be used to compute the priority for crops. The function must take an Crop object as input and must return an integer priority value. A typedef for the function pointer is provided for you in the header file:

  typedef int (*prifn_t)(const Crop&);

Overloaded Insertion Function

There is an overloaded insertion function for the class Crop to help you debugging the project. The implementation is provided to you. You do not need to modify the function.

Class Region

The class Region constructs a skew or a leftist data structure of the type min-heap or max-heap. This class has a member variable called m_heap. The member variable m_heap presents the root node of the heap data structure and it is of the type Crop. The following table presents the list of member functions that need implementation.

Class Irrigator

The class Irrigator constructs a complete tree heap data structure of the type min-heap. This class has a member variable called m_heap. The member variable m_heap points to the array that stores the heap data structure. The following table presents the list of member functions that need implementation.

• Private helper functions must be declared in the header file. No other modifications to the header file are permitted!
• No STL containers or additional libraries may be used in the implementation of the project classes. However, you can use STL containers in the Tester class for the testing purposes.
• The required functionality is provided in the Crop class. There is no need for any modifications to the implementation of this class.
• The test program must use the provided Random class to generate test data.
• Your code should not have any memory leaks or memory errors.
• In the case of a leftist heap the lowest level of nodes which store the keys have zero NPL value.
• Computed priority values may not be pre-computed and stored with the Crop object in the queue. They must be computed as needed using the priority function.
• Insertion to and extraction from the heap must run in amortized logarithmic time.
• Follow all coding standards as described on the C++ Coding Standards. In particular, indentations and meaningful comments are important.

• The test file name must be mytest.cpp; the file name must be in lower case, a file name like myTest.cpp is not acceptable.
• The test file must contain the declaration and implementation of your Tester class and the main() function as well as all your test cases, i.e. calls to your test functions.
• You are responsible for thoroughly testing your work before submission. The following section presents a non-exhaustive list of tests to perform on your implementation.
• You must write a separate function for every test case.
• Every test function must return true/false depending on passing or failing the test. Visual outputs are not accepted as test results.
• Tests cannot be interactive. The test file mytest.cpp must compile and run to completion.
• An example of declaring, implementing, and calling a test function, and outputting the test results was provided in the driver.cpp file of project 0.
• The testing guidelines page provides information that helps you to write more effective test cases.

Note: Testing incrementally makes finding bugs easier. Once you finish a function and it is testable, make sure it is working correctly.

Testing Region class

Note: The majority of tests need to check whether the heap property is satisfied after the operations. You might want to implement a helper function in your Tester class that performs such a functionality. Then, this helper can be called in multiple test functions.

• Test insertion for a normal case of min-heap. After a decent number of insertion (e.g. 300 nodes) we traverse the tree and check that the heap property is satisfied at every node.
• Test insertion for a normal case of max-heap. After a decent number of insertion (e.g. 300 nodes) we traverse the tree and check that the heap property is satisfied at every node.
• Test removal for a normal case of min-heap. After a decent number of insertion (e.g. 300 nodes) we check whether all removals happen in the correct order.
• Test removal for a normal case of max-heap. After a decent number of insertion (e.g. 300 nodes) we check whether all removals happen in the correct order.
• Test all nodes in a leftist heap have the correct NPL value.
• Test a leftist heap preserves the property of such a heap, i.e. at every node the NPL value of the left child is greater than or equal to the NPL value of the right child.
• Test whether after changing the priority function a correct heap is rebuilt with the same data (nodes) and the different priority function.
• Test merge of an empty queue (an edge case) with a normal queue. This is a call to the function Region::mergeWithQueue(Region& rhs) where rhs is a normally populated queue.
• Test the Region class copy constructor for a normal case.
• Test the Region class copy constructor for an edge case.
• Test the Region class assignment operator for a normal case.
• Test the Region class assignment operator for an edge case.
• Test that attempting to dequeue an empty queue throws an out_of_range exception.
• Test that attempting to merge queues with different priority functions throws a domain_error exception.

Random Numbers for Testing

For testing purposes, we need data. Data can be written as fixed values or can be generated randomly. Writing fixed data values might be a tedious work since we need a large amount of data points. You must use the provided Random class to generate test data.

In the file driver.cpp there is the class Random which generates pseudorandom numbers. The class is using a default seed value. On the same machine it always generates the same sequence of numbers. That is why the numbers are called pseudorandom numbers, they are not real random numbers. Please note, the numbers are machine dependent, therefore, the numbers you see in the sample file driver.txt might be different from the numbers your machine generates.

Memory leaks and errors

• Run your test program in valgrind; check that there are no memory leaks or errors.
  Note: If valgrind finds memory errors, compile your code with the -g option to enable debugging support and then re-run valgrind with the -s and --track-origins=yes options. valgrind will show you the lines numbers where the errors are detected and can usually tell you which line is causing the error.
• Never ignore warnings. They are a major source of errors in a program.

You must submit the following files to the proj3 directory.

• irrigator.h
• irrigator.cpp
• mytest.cpp (This file contains your Tester class, all test functions, all test cases, priority functions, and the main function.)

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using the following command:

   cp irrigator.h irrigator.cpp mytest.cpp ~/cs341proj/proj3/

For details of grading rubric please refer to Project Grading Policy